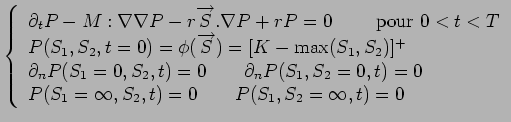 |
(1) |
Le problème à résoudre est le suivant :
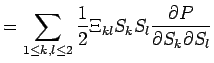 |
(2) | |
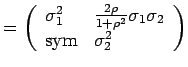 |
(3) |
Le problème est ensuite écrit sous forme divergence (...), tronqué sur le carré
![]() max
max![]() max
max![]() , écrit sous forme variationnelle (...).
, écrit sous forme variationnelle (...).
Puis, il est discrétisé en temps de façon semi-implicite2 :
En projetant cela sur une base
![]() d'éléments finis
d'éléments finis ![]() -Lagrange,
on en déduit le système linéaire :
-Lagrange,
on en déduit le système linéaire :
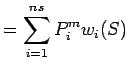 |
(6) | |
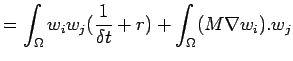 |
(7) | |
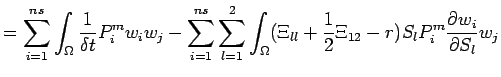 |
(8) |
Le problème européen (5) est résolu par l'algorithme suivant :
Pt, à l'instant Ag (qui est indépendante de Ft, et modifications dues aux conditions de Dirichlet.
L'algorithme est codé dans le programme BSeuro2D.cpp.
Il utilise les routines et objets de fem-V5, légèrement modifiés.