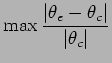| dans |
(1) | ||
| sur |
(2) | ||
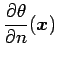 |
(3) | ||
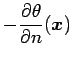 |
(4) |
Le but de ce projet est de créer un programme capable de résoudre l'équation de la chaleur suivante :
| dans |
(1) | ||
| sur |
(2) | ||
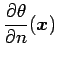 |
(3) | ||
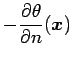 |
(4) |
Ce programme a été obtenu en adaptant le code de fem-v5 (écrit en C++ par F.Hecht), en lui ajoutant les possibilités de choisir la conductivité du matériau, ainsi que les conditions de Neumann et Fourier. Les résultats(3.1) sont présentés sous forme graphique.
Un deuxième programme aura pour but de traiter le même problème en 3 dimensions.
Pour ce projet, les résultats (voir la section 3.3) sont présentés sous forme ``brute'', c'est-à-dire un fichier contenant les valeurs de la solution aux différents points du maillage, et une petite synthèse de l'erreur dans le cas des tests : on note ![]() la solution exacte (théorique ?) et
la solution exacte (théorique ?) et ![]() celle calculée par le programme :
celle calculée par le programme :